mri pulses
Basics and characteristics of MRI pulses
The behavior of the magnetization is described by the Bloch equation (the relaxation is ignored here)
\[\text{Bloch equation}:\quad \frac{d\mathbf{M}}{dt} = \mathbf{M} \times \gamma \mathbf{B}\]where \(\mathbf{M}\) is magnetization, \(\gamma\) is gyromagnetic ratio, and \(\mathbf{B}\) is magnetic field.
Examples
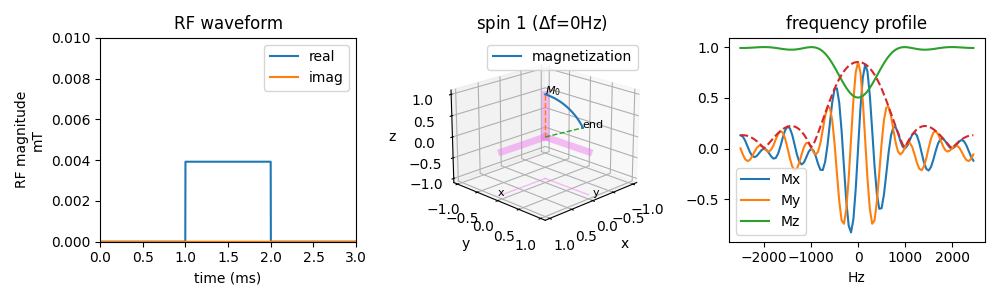
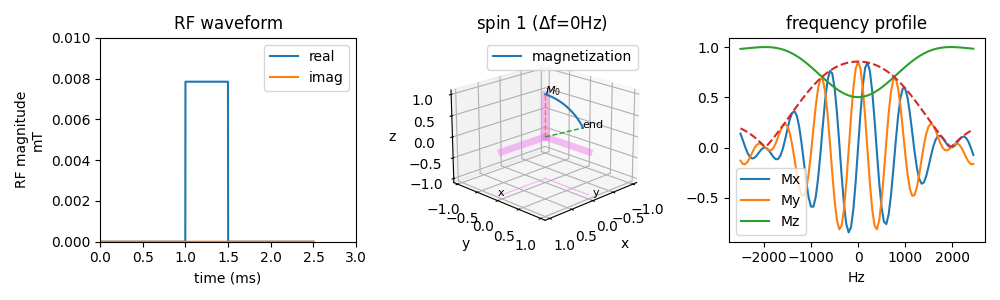
Rectangular pulse
The flip angle from a rectangular pulse can be computed using
\(\theta = \gamma B_1 T.\)
The square pulse is nonselective, but in frequency, it does have a different bandwidth for a different pulse duration,
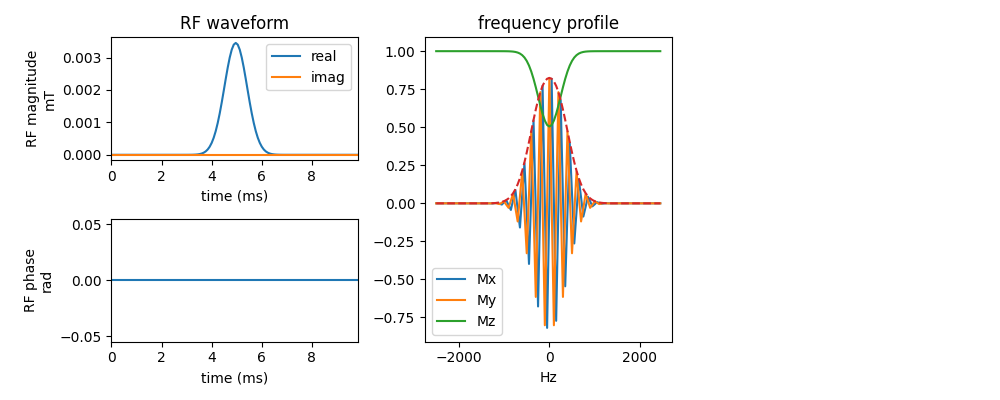
Gaussian pulse
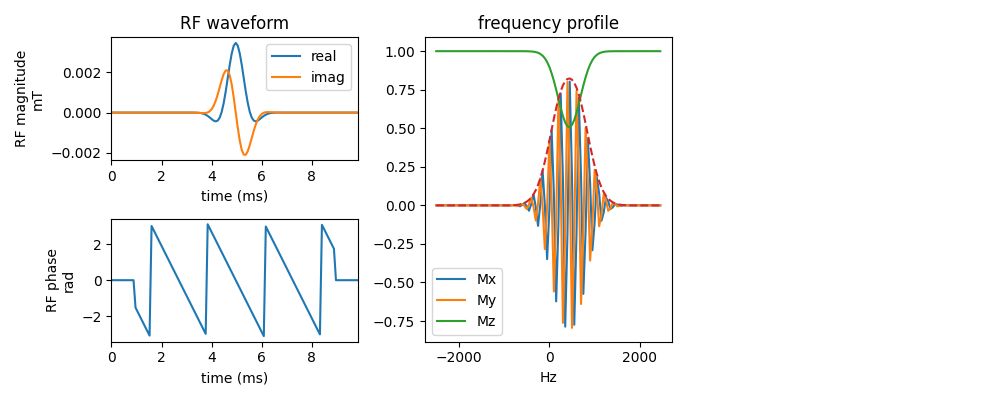
SINC
It is often mupltiplied by a window function. It can be used to select a slice with slice selective gradient. Things to control a sinc pulse
- time-bandwidth product, pulse duration (then the bandwidth can be computed)
- slice thickness (then the slice gradient can be determined)
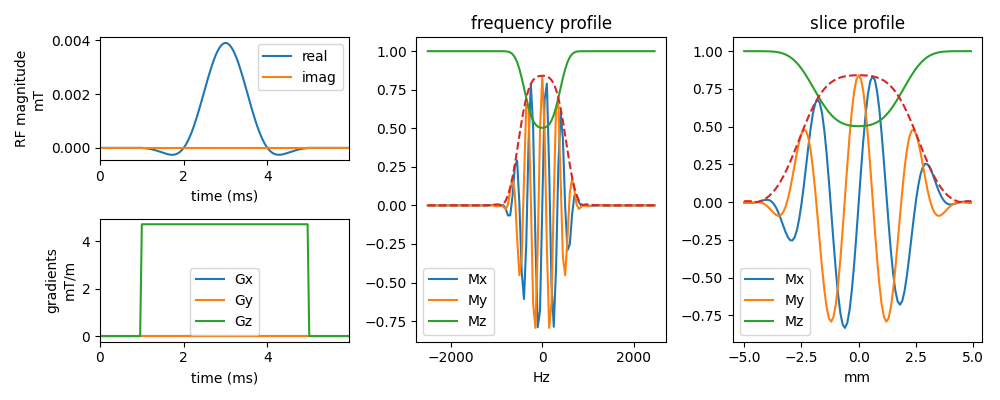
SLR
Shinnar-Le Roux pulse1.
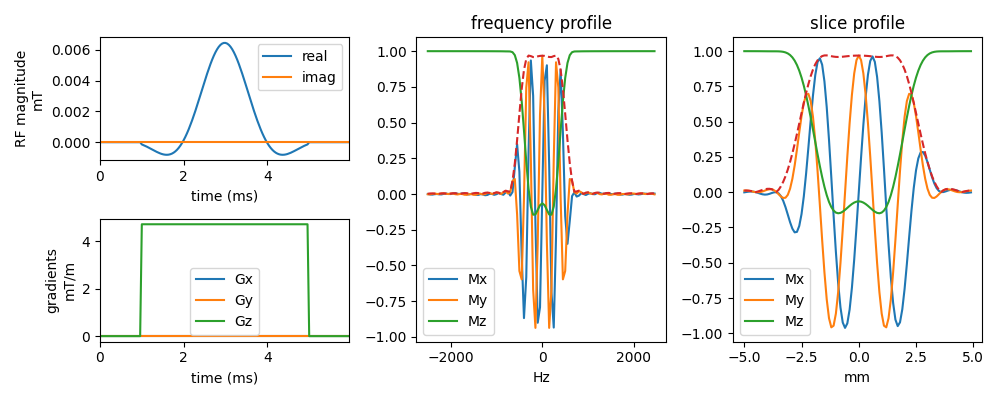
Adibatic pulse
-
Pauly, John, et al. “Parameter relations for the Shinnar-Le Roux selective excitation pulse design algorithm (NMR imaging).” IEEE transactions on medical imaging 10.1 (1991): 53-65. ↩